WillHou's Blog
0%

【题解】AcWing 第72场周赛题解

发表于 分类于 Valine：
AcWing 第72场周赛题解

忘打周赛了，亏了 30 分钟 /kk

离 AK 最近的一次，然而没有 /kk

A. 最小值

题目链接：AcWing 4624. 最小值

没啥好说的，题目意思都给你写在脸上了。

1
2
3
4
5
6
7
8
9
10
11
#include <iostream>
#include <algorithm>
int main() {
    int T, a, b;
    scanf("%d", &T);
    while (T--) {
        scanf("%d%d", &a, &b);
        printf("%d\n", std::min({a, b, (a+b)/3}));
    }
    return 0;
}

B. 压缩文件

题目链接：AcWing 4625. 压缩文件

比较显然的一道贪心。如果每一次都先压缩能够压缩最大空间的文件，则一定压缩的是最小次数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
#include <algorithm>
const int N = 1e5 + 9;
int n, m, ans;
long long sum;
struct Node {
    int x, y, dif;
} a[N];
int main() {
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) {
        scanf("%d%d", &a[i].x, &a[i].y);
        a[i].dif = a[i].x - a[i].y;
        sum += a[i].x;
    }
    std::sort(a + 1, a + n + 1, [](const Node &A, const Node &B) {
        return A.dif > B.dif;
    });
    if (sum <= m) {
        puts("0");
        return 0;
    }
    for (int i = 1; i <= n; i++) {
        sum -= a[i].dif;
        ans++;
        if (sum <= m) {
            printf("%d", ans);
            return 0;
        }
    }
    puts("-1");
    return 0;
}

PS. 这里可以不用结构体，但是我懒得再写一遍了。

C. 最小移动距离

题目链接：AcWing 4626. 最小移动距离

一道小思维题。一开始以为是宽搜，然后寄了。推出正确解法后，发现已经到时间了。我还是太菜了

先献个丑，贴出我周赛提交的代码（

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include <iostream>
#include <queue>
#include <cstring>
using namespace std;
const int N = 109;
int n, hd[N];
int f[N][N];
// f[i][j] 表示从 i 出发，移动 j 个距离到达
struct Edge {
    int to, nx;
} eg[N];
struct Node {
    int st, ed, stp;
};
void addE(int u, int v, int c) {
    eg[c] = {v, hd[u]}, hd[u] = c;
}
void bfs() {
    queue<Node> que;
    for (int i = 1; i <= n; i++)
        que.push({i, i, 0});
    while (que.size()) {
        Node node = que.front(); que.pop();
        int u = node.ed, steps = node.stp;
        if (steps > n) continue;
        for (int i = hd[u]; i; i = eg[i].nx) {
            int v = eg[i].to;
            // printf("(from %d)%d -> %d\n", node.st, u, v);
            f[node.st][steps+1] = v;
            que.push({node.st, v, steps+1});
        }
    }
}
int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        int x;
        scanf("%d", &x);
        addE(i, x, i);
    }
    bfs();
    // for (int i = 1; i <= n; i++) {
    //     for (int j = 1; j <= n; j++)
    //         printf("%-08d", f[i][j]);
    //     puts("");
    // }
    for (int j = 1; j <= n; j++) {// 枚举距离
        bool flag = true;
        for (int i = 1; i <= n; i++) {
            int t1 = f[i][j];
            int t2 = f[t1][j];
            // if (t1 and t2 and i==t2) continue;
            if (t1 and t2 and i==t2) {
                // printf("%d %d\n", t1, t2);
                continue;
            }
            // printf("%d %d\n", t1, t2);
            flag = false;
            break;
        }
        if (flag) {
            printf("%d", j);
            return 0;
        }
    }
    puts("-1");
    return 0;
}

一开始想当然地认为 \(t\) 的最大值为 \(n\)，然后就写出了如上代码。但是这个结论是显然错误的。反例：

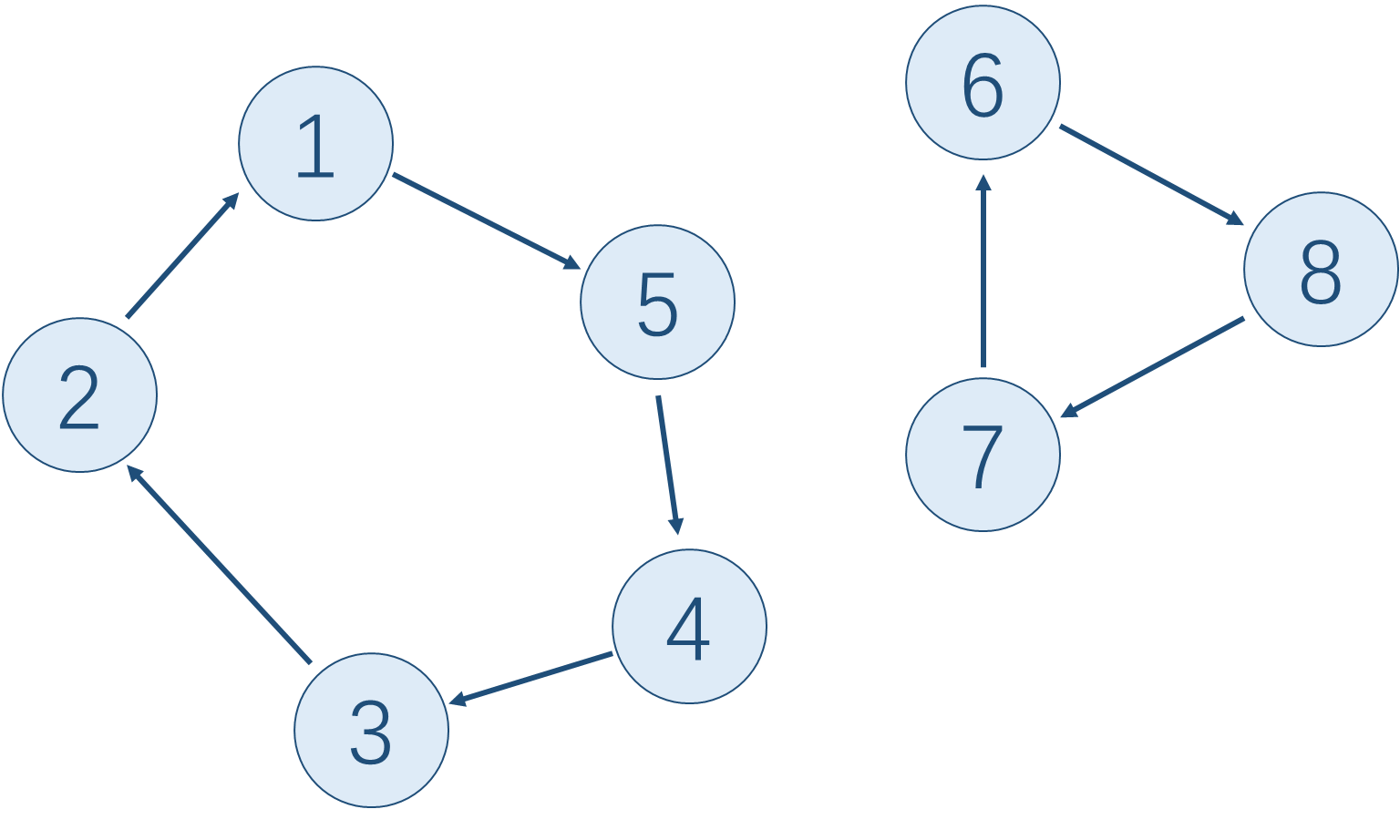
在该图中，\(t\) 应该等于 \(15\)，显然大于 \(8\)。

下面推导正确算法。

首先，我们可以先模拟一遍样例，观察规律。

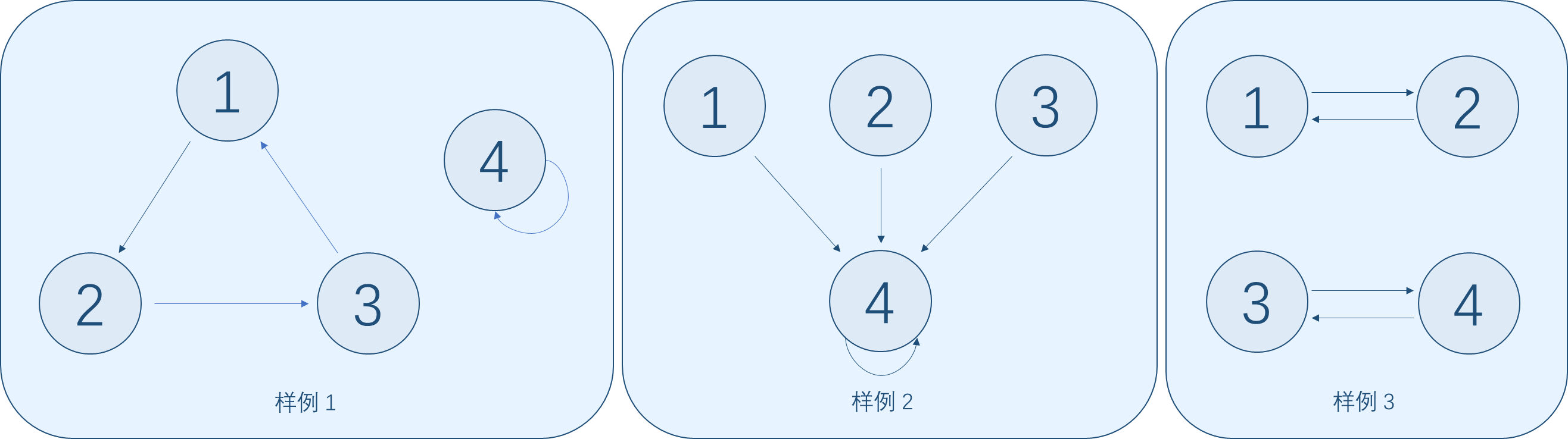
除了样例 \(2\) 无解，其他的都有解。可以发现，样例 \(2\) 的图不仅有环，还有树形结构。这种情况下无解。

但这样分析的话总有些不踏实——要是还有其他情况呢？

图无外乎有三种：树、链、环。所有图都可以由这三种结构组成。分别讨论这三种情况：

一. 树：由输入数据的格式可知，所有结点有且仅有一个出度。如果这个图中存在树，则一定有多个结点指向同一个结点。这种情况下，被指向的那个结点最多只能与指向它的一个结点相连，从而一定不能到达其它与之相连的点。所以，如果一个图中存在树形结构，则这个图不可能符合要求，输出 \(-1\)；

二. 链：首先，需要明确的是，这个图不可能是一个单纯的链，因为一条链只能有 \(n-1\) 条边，而输入中要有 \(n\) 条边。所以，这个图中必定至少存在一个树（分叉）或者环。由于是单向边，只要存在一个链，则链的终点一定无法连接到链的起点。所以这个图不可能符合要求，输出 \(-1\)；

三. 环：环的情况下， 容易得知，每个点必定可以在有限的次数中互相到达，有解。

综上所述，这个图必须由且仅由若干个环组成。

那么答案是多少呢？显然是这几个环的长度的最小公倍数。值得注意的是，它可能是绕一圈回到自己，也有可能是绕半圈到对面的点上。如果环的点数为偶数，则绕半圈即可；如果是奇数，则需要绕一圈回到自己。

现在，思路已经明确了。现在要想办法实现它。

通过上面的分析，我们发现需要我们实现的功能有两个：

  1. 判断这张图是否由若干个环组成；
  2. 统计每个环由多少个点构成。

当然，还有一个最小公倍数，但是这个是较为基础的模板，所以直接忽略不计了。

关于第一个功能，只需要判断每个点是否有且仅有一个入度就行了。

证明：显然成立。如果这个图中的其中一点有两个入度则有两种可能：

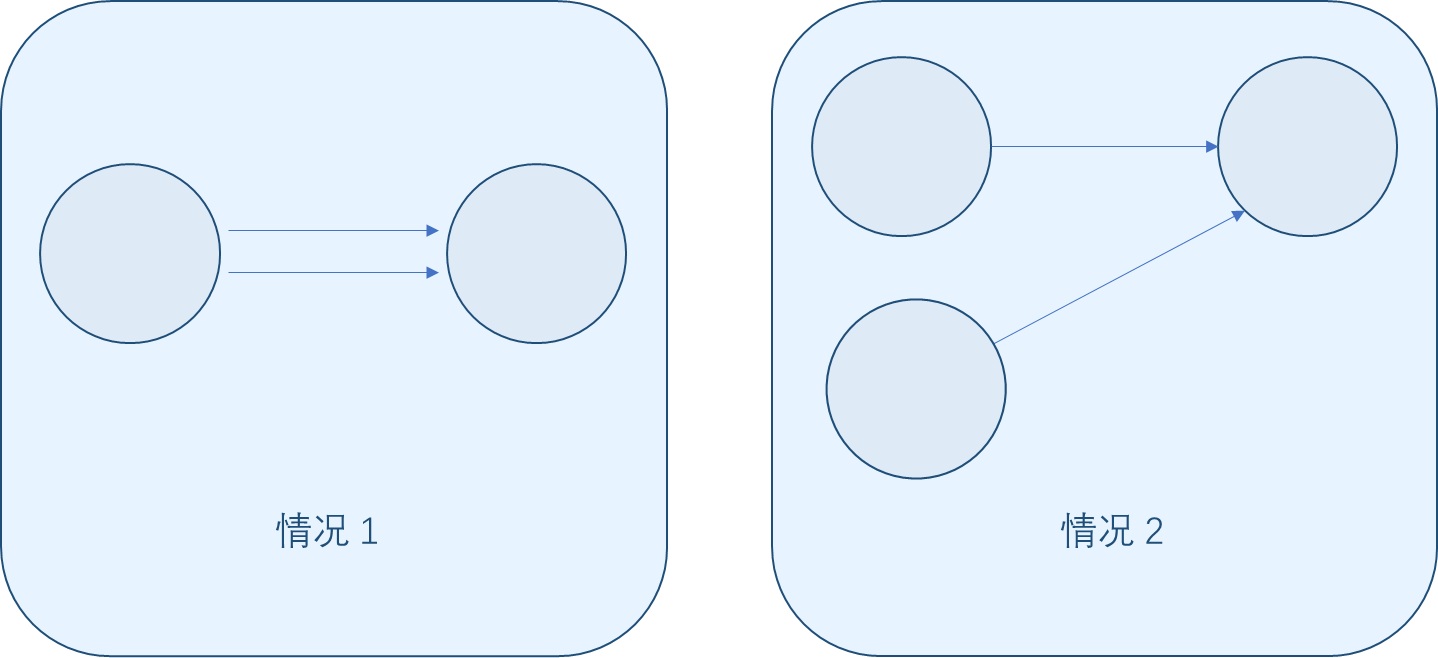
情况 \(1\) 在本题中是不可能的，因为每个结点最多只能有 \(1\) 个出度；情况 \(2\) 在前面的分析中已经被否决了。

所以，只需要统计每个点是否只有一个入度即可。

关于第二个功能，容易联想到 这道题，直接用差不多的方法统计一下就行了。

好了，这就是本题的分析过程。应该不能再详细了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include <iostream>
#include <cstring>
const int N = 109;
int n, ans = 1, cnt[N], ds[N];
int gcd(int a, int b) { return b==0 ? a : gcd(b, a%b); }
int lcm(int a, int b) { return a / gcd(a, b) * b; }
int find(int x) { return ds[x]<0 ? x : (ds[x] = find(ds[x])); }
void merge(int x, int y) {
    x = find(x), y = find(y);
    if (x == y) return ;
    if (ds[x] > ds[y]) std::swap(x, y);
    ds[x] += ds[y], ds[y] = x;
}
int main() {
    memset(ds, -1, sizeof ds);
    scanf("%d", &n);
    for (int i = 1, x; i <= n; i++) {
        scanf("%d", &x);
        merge(x, i);
        cnt[x]++;
        if (cnt[x] > 1) {
            puts("-1");
            return 0;
        }
    }
    for (int i = 1; i <= n; i++)
        if (ds[i] < 0) {
            int sz = -ds[i];
            if ((sz & 1) == 0) sz >>= 1;
            ans = lcm(ans, sz);
        }
    printf("%d", ans);
    return 0;
}