WillHou's Blog
0%

【专题】栈

发表于 分类于 Valine：
介绍了栈的基本操作、应用与经典题型

栈的定义

栈是限制插入和删除操作只能在一个位置上进行的表。它是一种 ==LIFO(Last In First Out)== 线性表。

表的末端成为栈的顶(top)

top

栈的操作与实现

数组实现

以下代码前提：

1
2
const int N = 1009; // 按需定
int stk[N], tp;

  1. push 操作(入栈)

    注意事项：入栈前务必要检查栈是否为满。

    不过，一般情况下，栈定义的大小总比题目中要求的大，所以可以不判断是否满。

    1
    2
    3
    4
    5
    6
    7
    bool push(int x) {
        if (tp == N)
            return false;
        // 以上代码可写可不写
       	stk[++tp] = x;
        return true;
    }

  2. pop 操作(出栈)

    注意事项：出栈前务必要检查栈是否为空。

    1
    2
    3
    4
    5
    6
    bool pop() {
        if (tp == 0)
            return false;
       	tp--;
        return true;
    }

  3. isEmpty 操作(判断栈是否为空)

    1
    2
    3
    bool isEmpty() {
        return tp == 0;
    }

  4. isFull 操作(判断栈是否为满)

    1
    2
    3
    bool isFull() {
        return tp == N;
    }

  5. size 操作(栈的大小)

    1
    2
    3
    int size() {
        return tp;
    }

  6. top 操作(返回栈顶元素的引用)

    1
    2
    3
    int top() {
        return stk[tp];
    }

  7. clear 操作(清空栈)

    1
    2
    3
    void clear() {
        tp = 0;
    }

STL 实现

使用前，必须加上头文件 #include <stack> & 标准名字空间 using std::stack;

示例代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include <iostream>
#include <stack>
using std::stack;
stack<int> stk;
int main() {
	int x = 10; // 待入栈元素
    stk.push(x); // 入栈操作
    printf("top=%d size=%d\n", stk.top(), stk.size()); // 返回栈顶指针的引用 & 栈的大小
    printf("isEmpty=%d\n", stk.empty()); // 返回栈是否为空
    if (!stk.empty()) stk.pop(); // 出栈操作
    printf("size=%d\n", stk.size()); // 返回栈的大小 *PS: 此处不能输出 stk.top() !
    printf("isEmpty=%d\n", stk.empty()); // 返回栈是否为空
    return 0;
}

以上函数的时间复杂度均为 \(O(1)\)

值得注意的是，STL 并没有清空栈的函数，所以，如果想要清空栈，只能这么写：

1
2
while (stk.size())
    stk.pop();

栈的应用

括号配对问题 / Easy

假设表达式中允许包含两种括号：圆括号和方括号，其嵌套的顺序随意，如 ( [ ] ( ) ) 或 [ ( [ ] [ ] ) ] 等为正确的匹配，[ ( ] ) 或( [ ] ( ) 或 ( ( ) ) ）均为错误的匹配。

现在的问题是，要求检验一个给定表达式中的括弧是否正确匹配？

输入一个只包含圆括号和方括号的字符串，判断字符串中的括号是否匹配，匹配就输出OK ，不匹配就输出Wrong。

题解

这题是最简单的括号配对问题。伪代码如下：

1
2
3
4
5
6
7
8
9
10
11
if (左括号) {
	入栈;
} else if (')') {
    if (栈顶不为'(')
        结束程序;
    出栈;
} else if (']') {
    if (栈顶不为'[')
        结束程序;
    出栈;
}

C++ 代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <iostream>
const int N = 1 << 8;
int tp;
char s[N], stk[N];
int main() {
    scanf("%s", s);
    for (int i = 0; s[i]; i++) {
        if (s[i]=='(' or s[i]=='[') {
            stk[++tp] = s[i];
        } else if (s[i] == ')') {
            if (stk[tp] != '(') {
                puts("Wrong");
                return 0;
            }
            tp--;
        } else if (s[i] == ']') {
            if (stk[tp] != '[') {
                puts("Wrong");
                return 0;
            }
            tp--;
        }
    }
    if (tp) puts("Wrong");
    else puts("OK");
    return 0;
}

括号配对问题 / Difficult

字符串中只含有括号 (),[],<>,{},判断输入的字符串中括号是否匹配。如果括号有互相包含的形式，从内到外必须是<>,(),[],{}，例如。输入: [()] 输出 YES，而输入([])，([)]都应该输出 NO。

PS. 本题为多组输入输出

题解

本题比上题难，主要难在两点：

  1. 括号种类 \(2\) 个增至 ==\(4\)== 个
  2. 引入==优先级==

其中，第一个难点可以通过定义字符串解决，第二个难点可以通过函数解决。题目整体难度不算大。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <iostream>
using namespace std;
const int N = 260;
int n, stk[N] = {8};
string s, priority = "<>()[]{}";
int get_pre(char c) {
    for (int i = 0; i < priority.size(); i++)
        if (priority[i] == c)
            return i;
}
int main() {
    ios::sync_with_stdio(false);
    cin.tie(0); cout.tie(0);
    cin >> n;
    while (n--) {
        int tp = 0;
        cin >> s;
        s = ' ' + s;
        int i, pre, len = s.size();
        for (i = 1; i <= len; i++) {
            pre = get_pre(s[i]);
            if ((pre & 1) == false) { // 左括号
                if (stk[tp] > pre) {
                    stk[++tp] = pre + 1; // 压入右括号(技巧)
                } else { // 优先级错误
                    puts("NO");
                    break;
                }
            } else {
                if (stk[tp] != pre) { // 括号不匹配
                    puts("NO");
                    break;
                } else { // 弹栈
                    tp--;
                }
            }
        }
        if (i < len) continue; // 已经 puts("NO");
        if (tp != 1) puts("NO"); // 有多余括号
        else puts("YES"); // 完全匹配且优先级正确
    }
    return 0;
}

简易计算器

小明在你的帮助下，破密了Ferrari设的密码门，正要往前走，突然又出现了一个密码门，门上有一个算式，其中只有“(”，“)”，“0-9”，“+”，“-”，“*”，“/”，“^”，求出的值就是密码。小明数学学得不好，还需你帮他的忙。(“/”用整数除法，"^"是幂运算，2^3 为 8)

PS. 输入保证合法

题解

读者可以先尝试这道题：洛谷_P1981 [NOIP2013 普及组] 表达式求值

本题是⌈表达式求值⌋的进阶版，具有一定的难度。

这题中，有如下运算符：(，)，+，-，*，/，^。由幼儿园知识易得，括号的运算优先级是最高的。所以，当我们遇到右括号时，就意味着从与它配对的左括号到它没有一个优先级比它高，这样就可以心安理得地弹栈并计算了。

那如果遇到了运算符呢？同理，不停弹栈并计算，直至栈顶运算符优先级比它高为止。

本题核心思想伪代码如下：

1
2
3
4
5
6
7
8
9
if (左括号) {
    将左括号压进符号栈;
} else if (右括号) {
    弹栈并计算;
} else if (数) {
    将其压进数字栈;
} else { // 即除括号外其他运算符
    弹栈直至栈顶运算符的优先级高于当前运算符的优先级;
}

C++ 代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
#include <iostream>
#include <cstring>
#include <cmath>
#include <cctype>
const int N = 39;
char s[N] = "(", stkc[N];
int stk[N], tp, tpc;
inline int pre(char op) {
    if (op=='+' or op=='-') return 1;
    if (op=='*' or op=='/') return 2;
    if (op=='^') return 3;
    return 0;
}
void calc() {
    int x = stk[tp--], y = stk[tp--];
    switch (stkc[tpc--]) {
        case '+': y += x; break;
        case '-': y -= x; break;
        case '*': y *= x; break;
        case '/': y /= x; break;
        case '^': y = pow(y, x); break;
    }
    stk[++tp] = y;
}
int read(int &cur) {
    int ans = 0;
    bool neg = false;
    char c = s[cur];
    if (c == '-') neg = true, ++cur;
    while (isdigit(s[cur])) ans = ans * 10 + s[cur++] - '0';
    cur--;
    return neg ? -ans : ans;
}
int main() {
    scanf("%s", s + 1);
    s[strlen(s)] = ')';
    for (int i = 0; s[i]; i++) {
        if (s[i] == '(') {
            stkc[++tpc] = '(';
        } else if (s[i] == ')') {
            while (stkc[tpc] != '(') calc();
            tpc--;
        } else if (isdigit(s[i]) or (s[i]=='-' and s[i-1]=='(')) { // 特别注意处理负数
            stk[++tp] = read(i);
        } else {
            while (pre(s[i]) <= pre(stkc[tpc])) calc();
            stkc[++tpc] = s[i];
        }
    }
    printf("%d", stk[tp]);
    return 0;
}

逆波兰表达式

逆波兰记法中，操作符置于操作数的后面。例如表达“三加四”时，写作“3 4 +”，而不是“3 + 4”。如果有多个操作符，操作符置于第二个操作数的后面，所以常规中缀记法的“3 - 4 + 5”在逆波兰记法中写作3 4 - 5 +”：先3减去4，再加上5。

使用逆波兰记法的一个好处是不需要使用括号。

PS. 保证式子正确，运算符只包括 加+、减-、乘*、除/

PS. 输出一个浮点数，保留两位有效数字

题解

按说这题比上题简单，因为没有什么乱七八糟的优先级问题。例如 1 2 + 3 *，当栈中有已经两个数，且当前字符为运算符，就 calc，否则继续压栈。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
#include <iostream>
#include <cstring>
#include <stack>
using namespace std;
stack <double> stk;
char s[1009], ch[109];
void calc(char c) {
	double x = stk.top(); stk.pop();
	double y = stk.top(); stk.pop();
	switch (c) {
		case '+': y += x; break;
		case '-': y -= x; break;
		case '*': y *= x; break;
		case '/': y /= x; break;
	}
	stk.push(y);
}
int main() {
	int cur = 0;
	cin.getline(s, 1009);
	s[strlen(s)] = ' ';
	for (int i = 0; s[i]; i++) {
		if (s[i] == ' ') continue;
		while ((s[i] >= '0' and s[i] <= '9') or s[i] == '.' or (s[i] == '-' and isdigit(s[i+1])))
            ch[cur++] = s[i++];
		if (isdigit(ch[0]) or ch[0] == '-') stk.push(atof(ch));
		else calc(s[i]);
		cur = 0;
		memset(ch, 0, sizeof(ch));
	}
	printf("%.2f", stk.top());
	return 0;
}

PS. 这个代码是以前写的，码风与其他代码不太一致，敬请谅解。

拓展 / 系统栈

利用递归写一个 \(10\) 进制转 \(2\) 进制的程序。

这个程序大家都会写：

1
2
3
4
5
6
void trans(int n) {
    if (n) {
        trans(n >> 1);
        printf("%d", n & 1);
    }
}

模拟将数 \(10\) 转为 \(2\) 进制的过程：

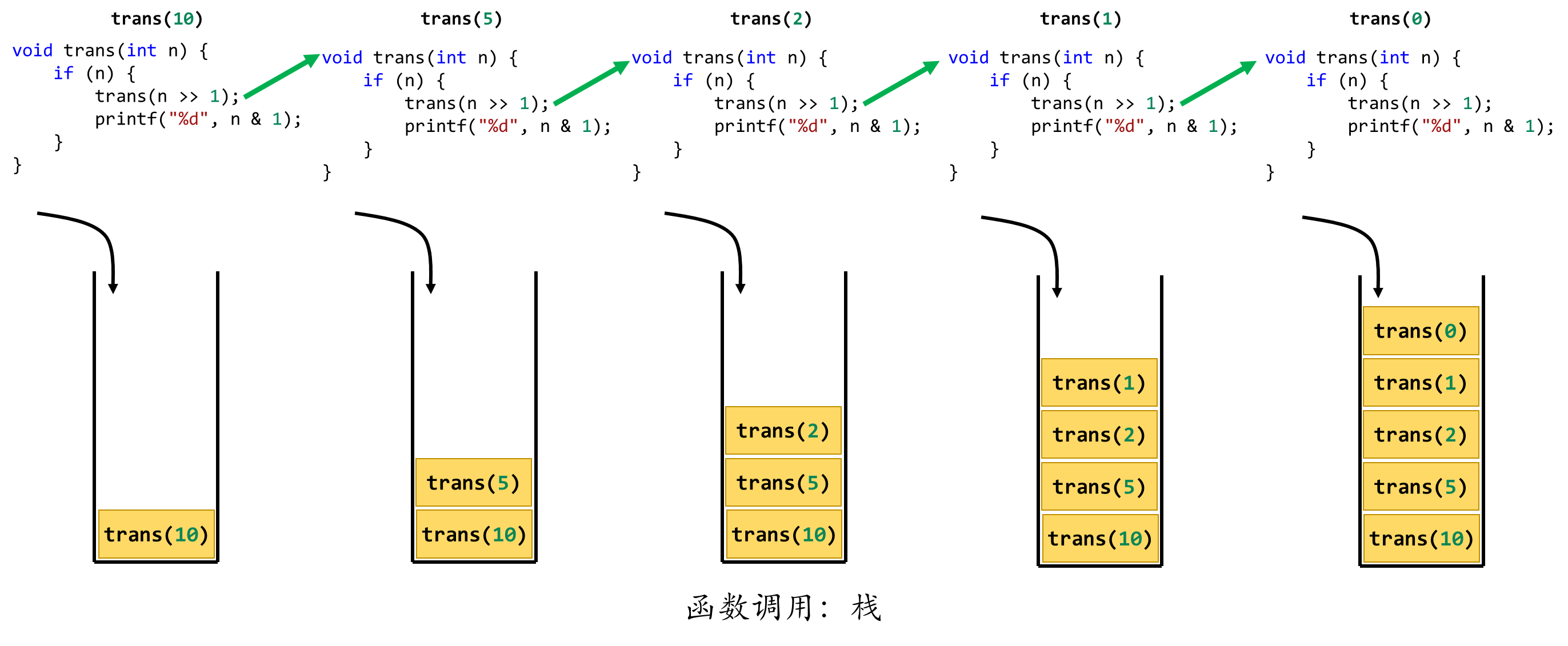ten2two

由上图，递归与回溯的过程其实就是压栈与弹栈。所以所有的 \(DFS\) 都可以用栈来解决。

下一篇文章将讲解 \(DFS\)