WillHou's Blog
0%

【专题】经典DP问题

发表于 分类于 Valine：
介绍了 10 道动态规划中的经典问题

1. 对抗赛(compete)

题目描述

程序设计对抗赛设有 \(N\) (\(0\lt N\lt 50\)的整数)个价值互不相同的奖品，每个奖品的价值分别为 \(S_1，S_2，S_3\dots S_n\)(均为不超过 \(100\) 的正整数)。现将它们分给甲乙两队，为了使得甲乙两队得到相同价值的奖品，必须将这 \(N\) 个奖品分成总价值相等的两组。

编程要求：对给定 \(N\) 及 \(N\) 个奖品的价值，求出将这 \(N\) 个奖品分成价值相等的两组，共有多少种分法？

例如：\(N = 5，S_1，S_2，S_3\dots S_n\) 分别为 \(1，3，5，8，9\)

则可分为 \(\{1，3，9\}\) 与 \(\{5，8\}\)

仅有 \(1\) 种分法；

例如：\(N = 7，S_1，S_2，S_3\dots S_n\) 分别为 \(1，2，3，4，5，6，7\)

则可分为：

\(\{1,6,7\}\) 与 \(\{2,3,4,5\}\)

\(\{2,5,7\}\) 与 \(\{1,3,4,6\}\)

\(\{3,4,7\}\) 与 \(\{1,2,5,6\}\)

\(\{1,2,4,7\}\) 与 \(\{3,5,6\}\)

有 \(4\) 种分法。

输入格式

输入包含 \(N\) 及 \(S_1，S_2，S_3\dots S_n\)。（每两个相邻的数据之间有一个空格隔开）。

输出格式

输出包含一个整数，表示多少种分法的答案，数据若无解，则输出 \(0\)。

解法分析

这题数据范围很小，所以写 dfs 都可以 AC。先上最好理解的 dfs:

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>
const int N = 59;
int n, sum, ans, a[N];
void dfs(int cur, int sub) {
    if (cur > (sum >> 1))
        return ;
    if (cur == (sum >> 1)) {
        ans++;
        return ;
    }
    for (int i = sub; i <= n; i++)
        dfs(cur+a[i], i+1);
}
int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++)
        scanf("%d", a + i), sum += a[i];
    if (sum & 1) {
        puts("0");
        return 0;
    }
    dfs(a[1], 2);
    printf("%d", ans);
    return 0;
}

dp 解法：不难看出，此题是一道 01背包 的求方案数类问题。每个奖品有选或者不选两种操作。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <iostream>
const int N = 5007, M = 50;
// f[i] 表示当 sum=i 时有多少种分法
int f[N], a[M];
int main() {
	int n, sum = 0;
	scanf("%d", &n);
	for (int i = 1; i <= n; i++)
		scanf("%d", a + i), sum += a[i];
	if (sum & 1) { puts("0"); return 0; }
	sum >>= 1;
	f[0] = 1;
	for (int i = 1; i <= n; i++)
		for (int j = sum; j >= a[i]; j--)
			f[j] += f[j-a[i]];
	printf("%d", f[sum]>>1);
	return 0;
}

2. 演讲大厅安排(hall)

题目描述

有一个演讲大厅需要我们管理，演讲者们事先定好了需要演讲的起始时间和中止时间。我们想让演讲大厅得到最大可能的使用。我们要接受一些预定而拒绝其他的预定，目标是使演讲者使用大厅的时间最长。假设在某一时刻一个演讲结束，另一个演讲就可以立即开始。

【编程任务】

  1. 输入演讲者的申请。

  2. 计算演讲大厅最大可能的使用时间。

  3. 将结果输出。

输入格式

输入第一行为一个整数 \(N(N≤5000)\)，表示申请的数目。

以下 \(n\) 行每行包含两个整数 \(p,k(1 ≤ p < k ≤ 30000)\)，表示这个申请的起始时间和中止时间。

输出格式

输出包含一个整数，表示大厅最大可能的使用时间。

解法分析

首先感谢出题人，latex用的少

这题是一道经典的线段覆盖问题。这种问题的固定解法是：

  1. 通过结构体记录每一段线段的头和尾
  2. 按照尾从小到大排序
  3. 使用 01背包 的解法解即可

代码如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include <iostream>
const int N = 1007;
int f[N], a[N];
int main()
{
	int n, sum = 0;
	scanf("%d", &n);
	for (int i = 1; i <= n; i++)
		scanf("%d", a + i), sum += a[i];
	if (sum & 1) { puts("0"); return 0; }
	sum >>= 1;
	f[0] = 1;
	for (int i = 1; i <= n; i++)
		for (int j = sum; j >= a[i]; j--)
			f[j] += f[j-a[i]];
	printf("%d", f[sum]>>1);
	return 0;
}

3. 火车票(railway)

题目描述

从 Ekaterinburg 到 Sverdlovsk 的火车线路上有若干个站点。这条线路可以近似的表示为一条线段，火车站就是线段上的点。线路始于 Ekaterinburg ，终于 Sverdlovsk。Ekaterinburg 被标号为 \(1\)，Sverdlovsk 被标号为 \(n\)。（\(n\) 为整条线路上的站点数）

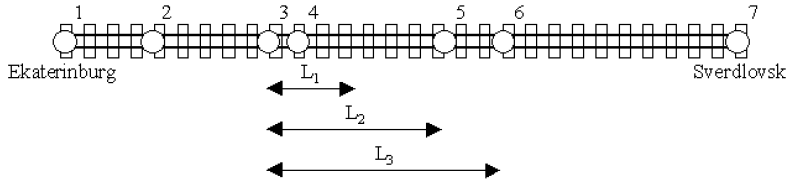
image.png

线路上的任意两个站点间的直达票价是由它们间的距离决定的，票价根据以下规则制定：

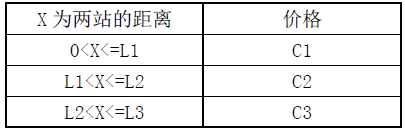
f3b685001d.png

如果两站的间距超过 \(L_3\)，则无直达车票。所以有时可能有必要买多张票，通过转车的方式，从一个站到达另一个站。

例如，在上面的图中，有 \(7\) 个站点。\(2\) 号站点到 \(6\) 号站点的距离超过 \(L_3\)，不能买直达票。存在若干种中转的方法，其中的一种是买两张票：先花费 \(C_2\) 从 \(2\) 号站到达 \(3\) 号站，然后花费 \(C_3\) 从 \(3\) 号站到 \(6\) 号站，一种花费 \(C_2+C_3\)。

你的任务是，找出一种最经济的中转方案。

输入格式

第一行 \(6\) 个整数 \(L_1, L_2, L_3, C_1, C_2, C_3\ (1\le L_1\lt L_2\lt L_3\le 10^9, 1\le C_1\lt C_2\lt C3\le 10^9)\)，中间用空格分隔。

第二行一个整数 \(n(2\le n\le 100)\)，表示线路上的车站数。

第三行两个整数 \(s\) 和 \(t\)，分别是起点和终点的编号。注意：\(s\) 不一定小于 \(t\)。

以下的 \(n-1\) 行，按据 Ekaterinburg 远近，每行描述了一个车站的位置。它包含一个整数，表示该车站距 Ekaterinburg 的距离。

任意两个车站的距离不超过 \(10^9\)，任意两个相邻的车站的距离不超过 \(L_3\)。

输出格式

一个整数，表示从给定的一个站到给定的另一个站的最小花费。

解法分析

这道题是一道典型的 区间DP 问题（可以把车站之间的距离看成一个物品）。

区间 DP 套路：

  1. 定状态：f[i][j]表示从 i~j 的区间（本题中表示从第 i 个车站到第 j 个车站最少花费多少钱）。
  2. 状态转移方程：f[i][j] = min(f[i][k] + f[k][j])

区间 DP 模式：

  1. 从小区间推至大区间（核心）

  2. 循环伪代码：

    1
    2
    3
    4
    5
    6
    for (区间长度) // 通常循环变量为 i
        for (起点) { // 通常循环变量为 j
            终点 = 起点 + 区间长度 - 1;
            for (断点) // 通常循环变量为 k
                状态转移方程;
        }

对于上面的代码，\(i,\ j,\ k\) 必须满足以下条件： \[ \begin{cases} k+1>i \\ [i, j] 的范围大于 [i, k],[k+1, j],因此要从小区间枚举到大区间 \end{cases} \] 由于在一般的 区间DP 的最小区间是 \(f[i][i]\)，所以通常会将其初始化(例如 合并石子)。当然，在一些 区间DP 的变式中，不一定这样初始化(例如本题)。

本题代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
#include <iostream>
#include <cstring>
typedef long long LL;
const int N = 109, INF = 0X3F3F3F3F3F3F3F3F;
LL f[N][N], L[N], C[N], loc[N];
LL calc(LL s)
{
	for (int i = 1; i <= 3; i++)
		if (s <= L[i]) return C[i];
	return INF;
}
int main()
{
	for (int i = 1; i <= 3; i++)
		scanf("%lld", L + i);
	for (int i = 1; i <= 3; i++)
		scanf("%lld", C + i);
	int n, s, t;
	scanf("%d%d%d", &n, &s, &t);
	memset(f, 0x3F, sizeof f);
	for (int i = 2; i <= n; i++)
	{
		scanf("%d", loc + i);
		f[i-1][i] = calc(loc[i] - loc[i-1]);
	}
	if (s > t) std::swap(s, t);
	// 区间 DP 第一层是枚举长度
	for (int d = 2; d <= n; d++)
		// 第二层枚举起点
		for (int i = 1; i+d-1 <= n; i++)
		{
			int j = i + d - 1;
			f[i][j] = calc(loc[j] - loc[i]);
			for (int k = i+1; k < j; k++)
				f[i][j] = std::min(f[i][j], f[i][k]+f[k][j]);
		}
	printf("%lld", f[s][t]);
	return 0;
}

4. 单词的划分(word)

题目描述

有一个很长的由小写字母组成字符串。为了便于对这个字符串进行分析，需要将它划分成若干个部分，每个部分称为一个单词。出于减少分析量的目的，我们希望划分出的单词数越少越好。你就是来完成这一划分工作的。

输入格式

第 \(1\) 行，一个字符串。（字符串的长度不超过 \(100\)）

第 \(2\) 行一个整数 \(n\)，表示单词的个数。（\(n<=100\)）

第 \(3\sim n+2\) 行，每行列出一个单词。

输出格式

一个整数，表示字符串可以被划分成的最少的单词数。

解法分析

这题是一道背包问题。把背包问题要素整理出来得：

  1. 背包容量：字符串长度
  2. 物品数：单词个数
  3. 物品价值：单词内容
  4. 物品体积：单词长度
  5. 物品数量：undefined

由此可以知道，本题是一道 01背包

代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#include <bits/stdc++.h>
using std::string;
const int N = 107;
std::map <string, bool> mp;
int f[N], n;
string s, w;
int main()
{
	memset(f, 0x3F, sizeof f);
	std::cin >> s >> n;
	for (int i = 1; i <= n; i++)
	{
		std::cin >> w;
		mp[w] = true;
	}
	if (mp[s.substr(0, 1)]) f[0] = 1;
	for (unsigned i = 1; i < s.size(); i++)
		for (int len = i+1; len; len--)
		{
			string ss = s.substr(i+1-len, len);
			if (mp[ss] == false) continue;
			if (i+1-len == 0) { f[i] = 1; break; }
			f[i] = std::min(f[i], f[i-len]+1);
		}
	std::cout << f[s.size()-1];
	return 0;
}

5. 饥饿的牛(hunger)

题目描述

牛在饲料槽前排好了队。饲料槽依次用 \(1\) 到 \(N(1\le N\le 2000)\) 编号。每天晚上，一头幸运的牛根据约翰的规则，吃其中一些槽里的饲料。

约翰提供 \(B\)B 个区间的清单。一个区间是一对整数 \(start-end(1\le start\le end\le N)\)，表示一些连续的饲料槽，比如 \(1\sim 3,7\sim 8,3\sim 4\) 等等。牛可以任意选择区间，但是牛选择的区间不能有重叠。

当然，牛希望自己能够吃得越多越好。给出一些区间，帮助这只牛找一些区间，使它能吃到最多的东西。

在上面的例子中，\(1\sim 3\) 和 \(3\sim 4\) 是重叠的；聪明的牛选择 \(\{1\sim3，7\sim 8\}\)，这样可以吃到 \(5\) 个槽里的东西。

输入格式

第 \(1\) 行，整数 \(B(1\le B\le 1000)\)。

第 \(2\sim B+1\) 行，每行两个整数，表示一个区间，较小的端点在前面。

输出格式

仅一个整数，表示最多能吃到多少个槽里的食物。

解法分析

这又是一道线段覆盖问题，分析见 演讲大厅安排(hall)

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>
#include <algorithm>
const int N = 2009;
int b, f[N];
struct Node {
    int st, ed;
} feed[N];
int main() {
	scanf("%d", &b);
    for (int i = 1; i <= b; i++)
        scanf("%d%d", &feed[i].st, &feed[i].ed);
    std::sort(feed + 1, feed + b + 1, [](const Node &a, const Node &b) {
        return a.ed<b.ed or (a.ed==b.ed and a.st<b.st);
    });
    int m = feed[b].ed;
    for (int i = 1; i <= b; i++) {
        for (int j = m; j >= feed[i].ed; j--)
            f[j] = std::max(f[j], f[feed[i].st-1] + feed[i].ed - feed[i].st + 1);
        // for (int j = 1; j <= m; j++)
        //     printf("%d ", f[j]);
        // puts("");
    }
    printf("%d", f[m]);
    return 0;
}

6. 数字游戏(game)

题目描述

丁丁最近沉迷于一个数字游戏。这个游戏看似简单，但丁丁在研究了许多天之后却发觉原来在简单的规则下想要赢得这个游戏并不那么容易。

游戏是这样的，在你面前有一圈整数（一共 \(n\) 个），你要按顺序将其分为 \(m\) 个部分，各部分内的数字相加，相加所得的 \(m\) 个结果对 \(10\) 取模后再相乘，最终得到一个数 \(k\)。游戏的要求是使你所得的 \(k\) 最大或者最小。

例如，对于下面这圈数字（\(n=4,m=2\)）：

1.png

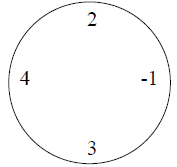
当要求最小值时， \[ ((2−1)\ mod\ 10)×((4+3)\ mod\ 10)=1×7=7 \] 要求最大值时，为 \[ ((2+4+3)\ mod\ 10)×(−1\ mod\ 10)=9×9=81 \] 特别值得注意的是，无论是负数还是正数，对 \(10\) 取模的结果均为非负值。

丁丁请你编写程序帮他赢得这个游戏。

输入格式

输入第一行有两个整数，\(n(1\le n\le 50)\) 和 \(m(1\le m\le 9)\)。

以下 \(n\) 行每行有一个整数，其绝对值不大于 \(10^4\)，按顺序给出圈中的数字，首尾相接。

输出格式

输出有两行，各包含一个非负整数。第一行是你程序得到的最小值，第二行是最大值。

解法分析

遇到这种环形区间DP时，我们采用破环成链的方法，即将链拷贝一份加在末尾

例如：4 3 -1 2 -> 4 3 -1 2 4 3 -1 2

1 2 3 4 5 6 7 8
4 3 -1 2 4 3 -1 2

长度最大为 N 的区间有 N 个，分别为 [1,n], [2,n+1], [3,n+2], ... ,[n,n+n-1]。我们最终在这 N 个情况中选择最优解。

其他的都不解释了，代码里注释比较清楚，有问题可以留言。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
#include <iostream>
#include <cstring>
const int N = 109, INF = 0x3F3F3F3F;
// f[i][j][z] 表示从 i 到 j 的部分，分成 z 份的最大值
// g[i][j][z] 表示从 i 到 j 的部分，分成 z 份的最小值
int f[N][N][10], g[N][N][10];
int n, m;
int main() {
    scanf("%d%d", &n, &m);
    memset(g, INF, sizeof g);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &f[i][i][1]);
        // 将所有的数全部转成大于等于0且小于等于10的整数
        f[i][i][1] = g[i][i][1] = (f[i][i][1]%10 + 10) % 10;
        // "破环成链"
        f[n+i][n+i][1] = g[n+i][n+i][1] = f[i][i][1];
    }
    // 求前缀和
    for (int i = 1; i < n+n; i++)
        for (int j = i+1; j <= n+n; j++)
            g[i][j][1] = f[i][j][1] = (f[i][j-1][1] + f[j][j][1]) % 10;
    for (int z = 2; z <= m; z++) // 枚举份数
        for (int i = 1; i <= n; i++) // 枚举左端点
            for (int j = i+z-1; j < i+n; j++) // 枚举右端点
                for (int k = i+z-2; k < j; k++) { // 枚举中间节点
                    g[i][j][z] = std::min(g[i][j][z], g[i][k][z-1] * g[k+1][j][1]);
                    f[i][j][z] = std::max(f[i][j][z], f[i][k][z-1] * f[k+1][j][1]);
                }
    // 求最大&最小值
    int mx = 0, mn = INF;
    for (int i = 1; i <= n; i++) {
        mx = f[i][i+n-1][m]>mx ? f[i][i+n-1][m] : mx;
        mn = g[i][i+n-1][m]<mn ? g[i][i+n-1][m] : mn;
    }
    printf("%d\n%d\n", mn, mx);
    return 0;
}

7. 能量项链(energy)

题目描述

在Mars星球上，每个Mars人都随身佩带着一串能量项链。在项链上有 \(N\) 颗能量珠。能量珠是一颗有头标记与尾标记的珠子，这些标记对应着某个正整数。并且，对于相邻的两颗珠子，前一颗珠子的尾标记一定等于后一颗珠子的头标记。因为只有这样，通过吸盘（吸盘是Mars人吸收能量的一种器官）的作用，这两颗珠子才能聚合成一颗珠子，同时释放出可以被吸盘吸收的能量。如果前一颗能量珠的头标记为 \(m\)，尾标记为 \(r\)，后一颗能量珠的头标记为 \(r\)，尾标记为 \(n\)，则聚合后释放的能量为 \(m\ast r\ast n\) （Mars单位），新产生的珠子的头标记为 \(m\)，尾标记为 \(n\)。

需要时，Mars人就用吸盘夹住相邻的两颗珠子，通过聚合得到能量，直到项链上只剩下一颗珠子为止。显然，不同的聚合顺序得到的总能量是不同的，请你设计一个聚合顺序，使一串项链释放出的总能量最大。

例如：设 \(N=4\)，\(4\) 颗珠子的头标记与尾标记依次为 \((2,3) (3,5) (5,10) (10,2)\)。我们用记号 \(\bigoplus\) 表示两颗珠子的聚合操作，\((j\bigoplus k)\) 表示第 \(j,k\) 两颗珠子聚合后所释放的能量。则第 \(4, 1\) 两颗珠子聚合后释放的能量为： \[ (4\bigoplus1)=10\times 2\times 3=60 \] 这一串项链可以得到最优值的一个聚合顺序所释放的总能量为 \[ ((4\bigoplus 1)\bigoplus 2)\bigoplus 3）=10\times 2\times 3+10\times 3\times 5+10\times 5\times 10=710 \]

输入格式

输入第一行是一个正整数 \(N(4\le N\le 100)\)，表示项链上珠子的个数。第二行是 \(N\) 个用空格隔开的正整数，所有的数均不超过 \(1000\)。第 \(i\) 个数为第 \(i\) 颗珠子的头标记\((1\le i\le N)\)，当 \(i<N\) 时，第 \(i\) 颗珠子的尾标记应该等于第 \(i+1\) 颗珠子的头标记。第 \(N\) 颗珠子的尾标记应该等于第 \(1\) 颗珠子的头标记。

至于珠子的顺序，你可以这样确定：将项链放到桌面上，不要出现交叉，随意指定第一颗珠子，然后按顺时针方向确定其他珠子的顺序。

输出格式

输出只有一行，是一个正整数 \(E(E≤2.1\times 10^9)\)，为一个最优聚合顺序所释放的总能量。

解法分析

这题仍然是一道环形DP问题，就不详细讲了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <iostream>
const int N = 209;
int n, f[N][N];
struct node {
    int x, y;
} a[N];
int main() {
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) {
        scanf("%d", &a[i].x);
        a[i+n].x = a[i].x, a[i-1].y = a[i+n-1].y = a[i].x;
    } a[2*n].y = a[1].x; // 初始化数组
    for (int len = 1; len <= n; len++)
        for (int i = 1; i+len < 2*n; i++) {
            int t = i + len;
            for (int k = i; k < t; k++)
                f[i][t] = std::max(f[i][t], f[i][k] + f[k+1][t] + a[i].x * a[k].y * a[t].y);
        }
    int ans = 0;
    for (int i = 1; i <= n; i++)
        ans = std::max(ans, f[i][i+n-1]);
    printf("%d", ans);
    return 0;
}

8. 传纸条(message)

题目描述

小渊和小轩是好朋友也是同班同学，他们在一起总有谈不完的话题。一次素质拓展活动中，班上同学安排做成一个 \(m\) 行 \(n\) 列的矩阵，而小渊和小轩被安排在矩阵对角线的两端，因此，他们就无法直接交谈了。幸运的是，他们可以通过传纸条来进行交流。纸条要经由许多同学传到对方手里，小渊坐在矩阵的左上角，坐标 \((1,1)\)，小轩坐在矩阵的右下角，坐标 \((m,n)\)。

从小渊传到小轩的纸条只可以向下或者向右传递，从小轩传给小渊的纸条只可以向上或者向左传递。

在活动进行中，小渊希望给小轩传递一张纸条，同时希望小轩给他回复。班里每个同学都可以帮他们传递，但只会帮他们一次，也就是说如果此人在小渊递给小轩纸条的时候帮忙，那么在小轩递给小渊的时候就不会再帮忙。反之亦然。

还有一件事情需要注意，全班每个同学愿意帮忙的好感度有高有低（注意：小渊和小轩的好心程度没有定义，输入时用 \(0\) 表示），可以用一个 \(0\sim 100\) 的自然数来表示，数越大表示越好心。小渊和小轩希望尽可能找好心程度高的同学来帮忙传纸条，即找到来回两条传递路径，使得这两条路径上同学的好心程度之和最大。现在，请你帮助小渊和小轩找到这样的两条路径。

输入格式

输入的第一行有 \(2\) 个用空格隔开的整数 \(m\) 和 \(n\)，表示班里有 \(m\) 行 \(n\) 列 \((1\le m,n\le 50)\)。

接下来的 \(m\) 行是一个 \(m\times n\) 的矩阵，矩阵中第 \(i\) 行 \(j\) 列的整数表示坐在第 \(i\) 行 \(j\) 列的学生的好心程度。每行的 \(n\) 个整数之间用空格隔开。

输出格式

输出共一行，包含一个整数，表示来回两条路上参与传递纸条的学生的好心程度之和的最大值。

解法分析

这道题难度较大，先定下状态：f[i][j][p][q] 表示 从小渊传到小轩的纸条到达 \((i,j)\)，从小轩传给小渊的纸条到达 \((p,q)\) 的路径上取得的最大的好心程度和 （这是坐标类DP的常见状态）

换句话说，即求第一张纸条到达 \((i,j)\)，第二纸条到达 \((p,q)\) 的路径上取得的最大的好心程度和，且两条路径严格不相交

所以，为了保证两条路径不重复，必须限制 \(q>j\)。如果不理解为什么这么限制，那么也可以让 \(q\) 从 \(1\) 开始枚举，但是需要判断 \((i,j)\) 与 \((p, q)\) 是否重合，若重合就把 \(f\) 数组转移后减掉 a[i][j] 或 a[p][q]。

时间复杂度 \(O(n^2\times m^2)\)，即最多 \(6250000\) 次计算，可以 AC

当然，可以优化这种算法。我们发现，\(i+j=p+q=step\) ，所以可以用 \(step\) 来表示其他两维，这样就实现了四维到三维的降维。这样，时间复杂度降低到 \(O(n^2\times (n+m))\)，即最多 \(250000\) 次计算，比上一种算法快 \(20\) 多倍。由于这种算法原理与第一种一样，就不给出代码（懒），供读者思考。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <iostream>
using std::max;
const int N = 55;
int m, n, a[N][N], f[N][N][N][N];
int max_of_four_ele(int liu, int rong, int sha, int bi) {
    return max(liu, max(rong, max(sha, bi)));
}
int main() {
    scanf("%d%d", &m, &n);
    for (int i = 1; i <= m; i++)
        for (int j = 1; j <= n; j++)
            scanf("%d", &a[i][j]);
    for (int i = 1; i <= m; i++)
        for (int j = 1; j <= n; j++)
            for (int p = 1; p <= m; p++)
                for (int q = j+1; q <= n; q++)
                    f[i][j][p][q] = max_of_four_ele(f[i-1][j][p-1][q], f[i][j-1][p-1][q], f[i-1][j][p][q-1], f[i][j-1][p][q-1]) + a[i][j] + a[p][q];
    printf("%d", f[m][n-1][m-1][n]);
    return 0;
}

9. 筷子(chop)

题目描述

A 先生有很多双筷子。确切的说应该是很多根，因为筷子的长度不一，很难判断出哪两根是一双的。这天，A 先生家里来了 \(K\) 个客人，A 先生留下他们吃晚饭。加上 A 先生，A 夫人和他们的孩子小 A，共 \(K+3\) 个人。每人需要用一双筷子。A 先生只好清理了一下筷子，共 \(N\) 根，长度为 \(T_1,T_2,T_3,\dots,T_N\)。

现在他想用这些筷子组合成 \(K+3\) 双，使每双的筷子长度差的平方和最小。(怎么不是和最小？？这要去问 A 先生了，呵呵)

输入格式

输入共有两行，第一行为两个用空格隔开的整数，表示 \(N,K(1≤N≤100, 0<K<50)\)，第二行共有 NN 个用空格隔开的整数，为 \(T_i\)。每个整数为 \(1\sim 50\) 之间的数。

输出格式

输出仅一行。如果凑不齐 \(K+3\) 双，输出 \(-1\)，否则输出长度差平方和的最小值。

解法分析

背包问题变形。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
#include <iostream>
#include <cstring>
#include <algorithm>
const int N = 107;
int n, k, a[N], f[N][N];
int main() {
    scanf("%d%d", &n, &k); k += 3;
    for (int i = 1; i <= n; i++)
        scanf("%d", a + i);
    if (k+k > n) { puts("-1"); return 0; }
    std::sort(a + 1, a + n + 1);
    memset(f, 0x3F, sizeof f);
    f[0][0] = 0;
    for (int i = 1; i <= k; i++)
        for (int j = i+i; j <= n; j++)
            f[i][j] = std::min(f[i][j-1], f[i-1][j-2] + (a[j]-a[j-1])*(a[j]-a[j-1]));
    printf("%d", f[k][n]);
    return 0;
}

10. 合并石子(merge)

题目描述

在一个操场上一排地摆放着 \(N\) 堆石子。现要将石子有次序地合并成一堆。规定每次只能选相邻的 \(2\) 堆石子合并成新的一堆，并将新的一堆石子数记为该次合并的得分。

试设计一个程序，计算出将 \(N\) 堆石子合并成一堆的最小得分。

输入格式

第一行为一个正整数 \(N\ (2\le N\le 100)\)；

以下 \(N\) 行,每行一个正整数，小于 \(10000\)，分别表示第 \(i\) 堆石子的个数。

输出格式

为一个正整数，即最小得分。

解法分析

这是一道最经典的区间DP了，真不知道为什么我要把这题拿到最后才讲。区间DP的解法在之前已经讲过了，这里不再赘述。点我跳转

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
#include <iostream>
#include <cstring>
const int N = 109, INF = 0x3F3F3F3F;
int n, s[N], f[N][N];
int main() {
	scanf("%d", &n);
    memset(f, INF, sizeof f);
    for (int i = 1; i <= n; i++)
        f[i][i] = 0;
    for (int i = 1; i <= n; i++)
        scanf("%d", s + i), s[i] += s[i-1];
    for (int i = n-1; i >= 1; i--)
        for (int j = i+1; j <= n; j++) {
            int t = s[j] - s[i-1];
            for (int k = i; k < j; k++)
                f[i][j] = std::min(f[i][j], f[i][k] + f[k+1][j] + t);
        }
    printf("%d", f[1][n]);
    return 0;
}