WillHou's Blog
0%

【专题】深搜算法

发表于 分类于 Valine：
深度优先搜索算法的详解

链接区

安利一发我的博客：WillHou's Blog

前言

之所以要把深搜(递归)放在栈后面写，是因为深搜的本质就是一个栈。

当我们递归地实现 DFS 时，似乎不需要使用任何栈。但实际上，我们使用的是由系统提供的隐式栈，也称为调用栈（Call Stack）。—— CSDN 大佬 却把清梅嗅

深搜的优点：

  • 代码量小
  • 可读性强
  • 更容易实现

深搜的缺点：

  • 如果深度太高，容易发生栈溢出
  • 容易超时

深搜的使用场景：

  • 在图论中大量使用（实际上深搜的概念就是基于图论的，只不过我们通常把深搜的概念广义化）
  • 当你实在做不出来时骗分

概念

DFS 全称是 Depth First Search，中文名是深度优先搜索，是一种用于遍历或搜索树或图的算法。所谓深度优先，就是说每次都尝试向更深的节点走。DFS 常常用来指代用递归函数实现的搜索，但实际上两者并不一样。

应用

先来一个不是这么正经的，感受一下何为递归。

1
2
3
4
5
6
7
8
9
#include <iostream>
void tellStory() {
	puts("从前有座山，山上有座庙，庙里有个老和尚在讲故事，讲的故事是：");
    tellStory();
}
int main() {
    tellStory();
	return 0;
}

这个程序永远无法终止，会不停的输出“从前有座山，山上有座庙，庙里有个老和尚在讲故事，讲的故事是：”。

当然，这样的程序完全没有用处。所以，我们尝试对它加入次数限制：

1
2
3
4
5
6
7
8
9
10
#include <iostream>
void tellStory(int times) {
    if (!times) return ;
	puts("从前有座山，山上有座庙，庙里有个老和尚在讲故事，讲的故事是：");
    tellStory(times-1);
}
int main() {
    tellStory(10);
	return 0;
}

这样，我们限制它只输出十次。那如果我也想看到这是第几次输出呢？

1
2
3
4
5
6
7
8
9
10
#include <iostream>
void tellStory(int times) {
    if (!times) return ;
	printf("%d. 从前有座山，山上有座庙，庙里有个老和尚在讲故事，讲的故事是：\n", 11 - times);
    tellStory(times-1);
}
int main() {
    tellStory(10);
	return 0;
}

这样，我们基本得到了一个递归(DFS) 的模板（伪代码）：

1
2
3
4
5
6
7
8
void dfs(int argument) {
    if (结束条件满足) {
        如果有，就操作;
        return ;
    }
    当层要做的事情;
    递归到下一层;
}

例题

斐波那契数列

概括：求斐波那契数列的第 \(n\) 项，第一项为 \(0\)，第二项为 \(1\)。

关于斐波那契数列的定义，请出门右转到百度百科。

这是一道典型的递归题，可以直接套用上面的模板。

1
2
3
4
5
6
7
8
9
10
11
12
#include <cstdio>
int cnt = 2, temp;
int fbi(int m) {
	if (m <= 2) return m - 1; // 这句是用了点技巧，请手算推之。
	return fbi(m-1) + fbi(m-2);
}
int main() {
	int n;
	scanf("%d", &n);
	printf("%d", fbi(n));
	return 0;
}

最大公约数

概括：求两个正整数 \(a\) 和 \(b\) 的最大公约数。

关于最大公约数的定义，请出门右转到百度百科。

这是众所周知的辗转相除法，也是入门必备小技巧之一。

关于辗转相除法的原理，请出门右转到百度百科

看完百度百科的你一定发现了，这其实就是递归的过程。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <cstdio>
int gcd(int a, int b) { return b==0 ? a : gcd(b, a%b); }
/*
这看上去不符合递归(深搜)的模板，但当你整理成这样后：
int gcd(int a, int b) {
	if (b == 0) return a;
	return gcd(b, a%b);
}
你就会发现这还是一模一样的。
*/
int main()
{
	int m, n;
	scanf("%d%d", &m, &n);
	printf("gcd=%d", gcd(m, n));
	return 0;
}

全排列问题

概括：给定一个由不同的小写字母组成的字符串，输出这个字符串的所有全排列。 输入已经按照字典序整理好。

关于全排列的定义，请出门右转到百度百科。

这道题是进阶的 DFS。还包括了搜索中重要的技巧：回溯法。如果说递归(DFS)是一种“不撞南墙不回头”的算法，那么回溯法就是让他回头。比如我们要达到一个目的地，但是我们面前有三条路，并且只有一条路是可以到达目的地的，因此我们需要一条一条去尝试，如果不行的话就得回到原点，选择下一条路进行尝试，这种就叫做回溯。

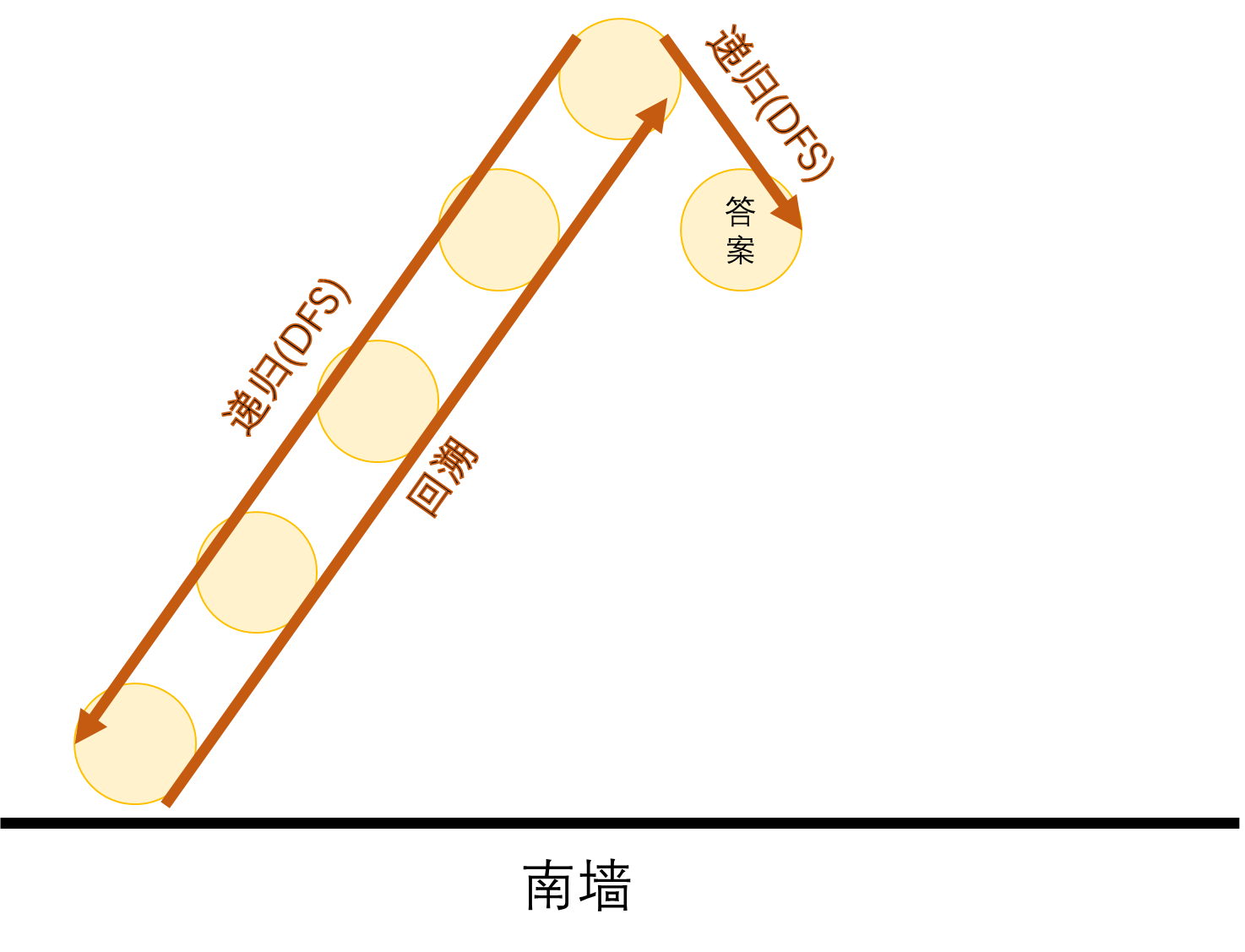
其工作原理为：

  1. 构造空间树；
  2. 进行遍历；
  3. 如遇到边界条件，即不再向下搜索，转而搜索另一条链；
  4. 达到目标条件，输出结果。

其模板为（伪代码）：

1
2
3
4
5
6
7
8
9
10
void dfs(int argument) {
    if (结束条件满足) {
        如果有，就操作;
        return ;
    }
    当层要做的事情;
    标记为已访问;
    递归到下一层;
    标记为未访问;
}

代码灵活性强，没有特别绝对的模板，需要 OIer 灵机应变。

关于这题的代码，请出门调头到 CSDN 或 我的博客

参考文献

  1. OI-Wiki: https://oi-wiki.org/